Απλή αρμονική ταλάντωση με τη χρήση του MultiLog (& video)
Απλή αρμονική ταλάντωση με τη χρήση του MultiLog (Γ? Τάξη ? Θετική και Τεχνολογική Κατεύθυνση)
Απλή αρμονική ταλάντωση με τη χρήση του MultiLog (βίντεο ![]() )
)
Απλή αρμονική ταλάντωση με τη χρήση του MultiLog
(Γ? Τάξη ? Θετική και Τεχνολογική Κατεύθυνση)
ΥΛΙΚΑ ΠΟΥ ΑΠΑΙΤΟΥΝΤΑΙ:
1. Βάση παραλληλόγραμμη (ΓΕ.010.0)
2. Δύο ράβδοι 60 ή 80cm (ΓΕ.030.2 ή 3, αποφεύγουμε του 1m γιατί δεν είναι πολύ σταθερή)
3. Δύο σύνδεσμοι απλοί (ΓΕ.020.0)
4. Δύο σφιγκτήρες τύπου G (ΓΕ.050.0), για στερέωση της παραλληλόγραμμης βάσης
5. Ένα ελατήριο (ΜΣ.020.0)
6. Μάζες (βαράκια) (ΓΕ.100.Χ)
7. Ζυγός ηλεκτρονικός (ΓΕ.130.0), για τη μέτρηση της μάζας
8. MultiLog (Data Logger) ? Συγχρονική διάταξη φορητή, κεντρική μονάδα (ΛΑ.610.0)
9. Αισθητήρας δύναμης (ΛΑ.620.0), καλώδιο (sensor cable) και προσαρμοστή αισθητήρων (VERNIER sensor adapter)
10. Αισθητήρας απόστασης (ΛΑ.625.0) και καλώδιο (sensor cable)
11. Η/Υ με εγκατεστημένο το λογισμικό DB-Lab 3.2, για επεξεργασία των μετρήσεών μας.
ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ:
- Οι παρακάτω οδηγίες δίνονται έχοντας το MultiLog συνδεδεμένο στον Η/Υ και βλέποντας απ? ευθείας ότι καταγράφεται στην οθόνη του υπολογιστή, μέσω του προγράμματος DB-Lab 3.2.
- Οι ενδείξεις «?» αντιστοιχούν σε επιλογές πλήκτρων και οι ? σε επιλογές μέσα σε ανοικτά παράθυρα του λογισμικού.
- Προσέχουμε όταν τελειώσουμε τις μετρήσεις μας να απομακρύνουμε τη μάζα από το ελατήριο (και τον αισθητήρα απόστασης από το δάπεδο), για να αποφύγουμε τον κίνδυνο να πέσει κατά λάθος πάνω στον αισθητήρα και να τον καταστρέψει.
- Αν τυχόν ο αισθητήρας απόστασης δεν δείχνει ενδείξεις, σημαίνει (με μεγάλη πιθανότητα) ότι τα δύο μικρά κλιπς-επαφές που έχει στο εσωτερικό του έχουν μετακινηθεί από τη θέση τους. Με σχετική ευκολία μπορούμε να ανοίξουμε το κάλυμμα του αισθητήρα και να τα συνδέσουμε ξανά.
- Η ταλάντωση της μάζας να έχει πλάτος τέτοιο, ώστε να μην συσπειρώνεται ως το ανώτερο τμήμα του το ελατήριο.
- Αν το ελατήριο που χρησιμοποιούμε είναι αρκετά σκληρό και η μάζα μεγάλη, π.χ. 1Kg, τότε χρησιμοποιούμε τις ενδείξεις του αισθητήρα δύναμης όπως στο παρακάτω υπόδειγμα της πειραματικής διαδικασίας. Αν όμως το ελατήριο είναι μαλακό και η μάζα μικρή πρέπει να προσέξουμε ιδιαιτέρως μήπως ο αισθητήρας δείχνει κάποια αρχική ένδειξη χωρίς φορτίο ή με φορτίο μόνο το ελατήριο, γιατί επηρεάζει σημαντικά τις μετρήσεις μας (δες σημείωση στο τέλος της πειραματικής διαδικασίας).
ΠΕΙΡΑΜΑΤΙΚΗ ΔΙΑΔΙΚΑΣΙΑ:
1. Ζυγίζουμε τη μάζα.
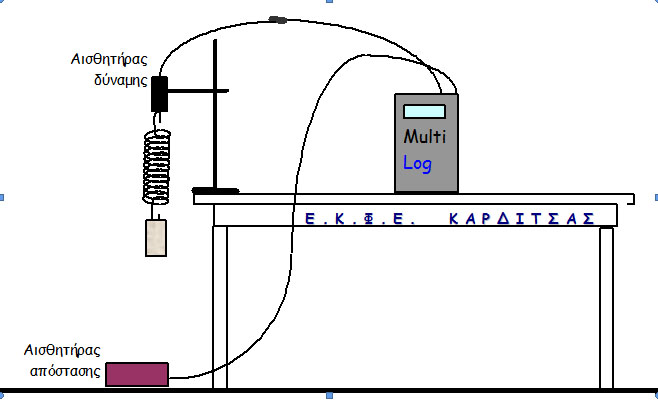
2. Συναρμολογούμε τη διάταξη του διπλανού σχήματος.
3. Βάζουμε στο κάτω μέρος του ελατηρίου τη μάζα και αφήνουμε να ισορροπήσει.
4. Ο αισθητήρας κίνησης φροντίζουμε να είναι σχετικά μακριά από το τραπέζι, από εμάς ή από ότι πιθανόν κινείται γιατί καταγράφει κινήσεις με γωνία λήψης 20?.
5. Συνδέουμε στην υποδοχή Ι/Ο-1 τον αισθητήρα κίνησης (ή απόστασης ή διαστήματος - DST) και στην υποδοχή Ι/Ο-2 τον αισθητήρα δύναμης.
6. Ανοίγουμε το MultiLog από το πλήκτρο ΟΝ και ελέγχουμε αν αναγνώρισε τους αισθητήρες (από τα πλήκτρα PORT και SENSOR). Αν δεν τους αναγνώρισε (που έτσι συμβαίνει τις περισσότερες φορές), από το λογισμικό DB-Lab 3.2. επιλέγουμε «Καταγραφέας», «Πίνακας Ελέγχου», Είσοδος 1 " Διάστημα [στην οθόνη του MultiLog γράφει Distance], Είσοδος 2 " Force_10 [στην οθόνη του MultiLog γράφει My Sensors] ή Δύναμη (SFS) [στην οθόνη του MultiLog γράφει Force].
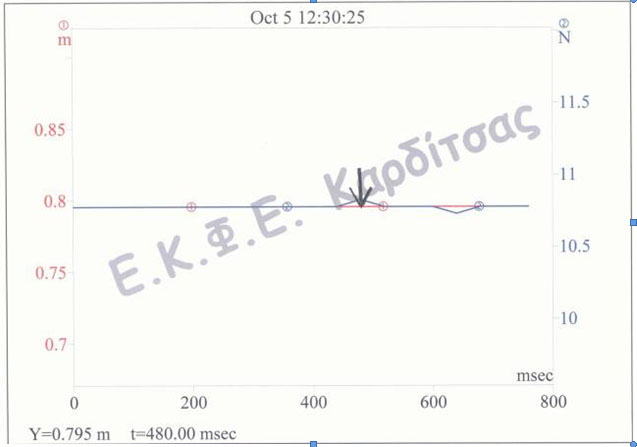
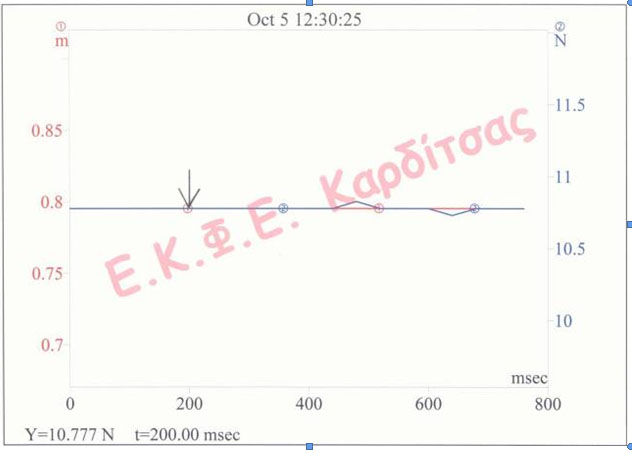
7. Στο παράθυρο του «Πίνακα Ελέγχου», που είναι ανοικτό επιλέγουμε Σημεία " 20, Ρυθμός " 10/sec και «Λήψη Δεδομένων». Εμφανίζεται μια γραφική παράσταση που μας δίνει την αρχική θέση x0 και την αρχική δύναμη F0 στη θέση ισορροπίας. Με διπλό κλικ στην γραμμή (καμπύλη) που αντιστοιχεί στο x εμφανίζεται κάτω από τη γραφική παράσταση η τιμή της x0 (π.χ. Υ=0,795m). Με διπλό κλικ στην γραμμή που αντιστοιχεί στην F εμφανίζεται κάτω από τη γραφική παράσταση η τιμή της F0 (π.χ. Υ=10,777N). Σημειώνουμε τις τιμές αυτές. Στη συνέχεια αποθηκεύουμε αυτή τη γραφική παράσταση («Αρχείο», «Αποθήκευση ως?») με όνομα που δεν θα έχει περισσότερους από οκτώ χαρακτήρες (π.χ. αατ1).
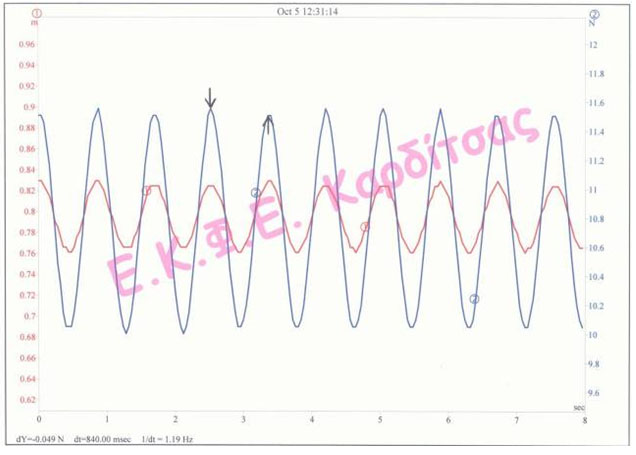
8. Θέτουμε το σώμα σε ταλάντωση, περιμένουμε μερικά δευτερόλεπτα να σταθεροποιηθεί και στο παράθυρο «Πίνακας Ελέγχου», που είναι ανοικτό επιλέγουμε Σημεία " 100 ή 200, Ρυθμός " 25/sec και «Λήψη Δεδομένων». Εμφανίζεται μια γραφική παράσταση που στον άξονα Χ έχει χρόνο σε sec και στον Υ αριστερά την απόσταση σε m και δεξιά τη δύναμη σε Ν. Έχουμε πάρει τη γραφική παράσταση που μας δείχνει την ημιτονοειδή μεταβολή των μεγεθών που μελετούμε. (Όμως δύναμη και απόσταση δείχνουν συμφασικά μεγέθη, ενώ γνωρίζουμε ότι είναι σε αντίθεση φάσης, F=-Dx. Αυτό οφείλεται στο ότι ο αισθητήρας δύναμης καταγράφει τη δύναμη που αυτός δέχεται και είναι αντίθετη από αυτή που δέχεται το σώμα.)
9. Με διπλό κλικ τσεκάρουμε δύο διαδοχικά μέγιστα ή ελάχιστα της καμπύλης και βρίσκουμε την περίοδο της ταλάντωσης Τ (π.χ. dt=840,00msec).
10. Για να διορθώσουμε το ?παράδοξο? του βήματος 8 ακολουθούμε την εξής διαδικασία:
α) «Ανάλυση», «Περισσότερα?», στο παράθυρο «Επεξεργασία» στο κουτάκι G1 Επιλέξατε " Δύναμη (SFS)_I/O-2 και OK. Στο κουτάκι Συνάρτηση επιλέγουμε " Γραμμική, στο C1 γράφουμε -1 και στο C2 την τιμή της F0=10,777 και OK.
Εμφανίζεται μια νέα γραφική παράσταση με τίτλο Γραμμική (Δύναμη (SFS)_I/O-2).
β) «Ανάλυση», «Περισσότερα?», στο παράθυρο «Επεξεργασία» στο κουτάκι G1 Επιλέξατε " Διάστημα_I/O-1 και OK. Στο κουτάκι Συνάρτηση επιλέγουμε " Γραμμική, το C1 το αφήνουμε 1 και στο C2 την τιμή της x0=0,795 και OK .
Εμφανίζεται μια νέα γραφική παράσταση με τίτλο Γραμμική (Διάστημα_I/O-1).
γ) Ενώ έχουμε επιλεγμένη την γραφική παράσταση Γραμμική (Διάστημα_I/O-1) κάνουμε κλικ στο «Επεξεργασία», «Αντιγραφή» και αφού επιλέξουμε την Γραμμική (Δύναμη (SFS)_I/O-2) κάνουμε κλικ στο «Επεξεργασία», «Επικόλληση». Εμφανίζεται μια γραφική παράσταση με τίτλο Γραμμική (Δύναμη (SFS)_I/O-2), όπου συνυπάρχουν οι μεταβολές της δύναμης και της απόστασης σε αντίθεση φάσης.
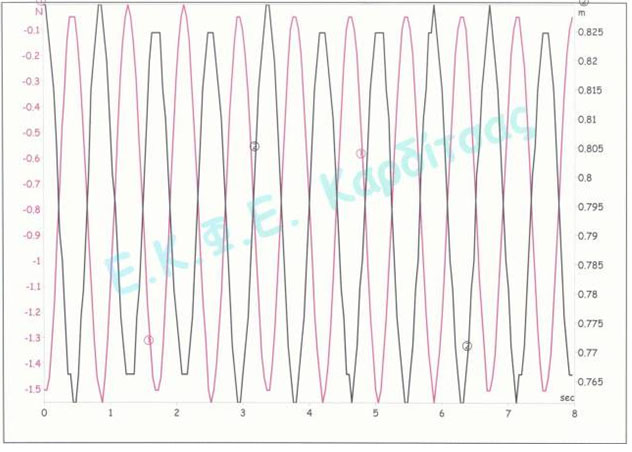
11. Αν θέλουμε να αλλάξουμε την κλίμακα κάνουμε την εξής διαδικασία:
α) «Προβολή», «Κλίμακα?», στο «Επιλογή Δεδομένων» κλικ στο Γραμμική (Δύναμη (SFS)_I/O-2) και ΟΚ. Στο νέο παράθυρο «Κλιμάκωση» γράφουμε Ελάχιστο " -2, Μέγιστο " 0,5, Υποδιαιρέσεις " 11 και ΟΚ.
β) «Προβολή», «Κλίμακα?», στο «Επιλογή Δεδομένων» κλικ στο Γραμμική (Διάστημα_I/O-1) και ΟΚ. Στο νέο παράθυρο «Κλιμάκωση» γράφουμε Ελάχιστο " 0,7, Μέγιστο " 0,9, Υποδιαιρέσεις " 11 και ΟΚ. (Την υποδιαστολή την σημειώνουμε με τελεία, όχι κόμμα, δηλ. 0.7 κ.ο.κ.)
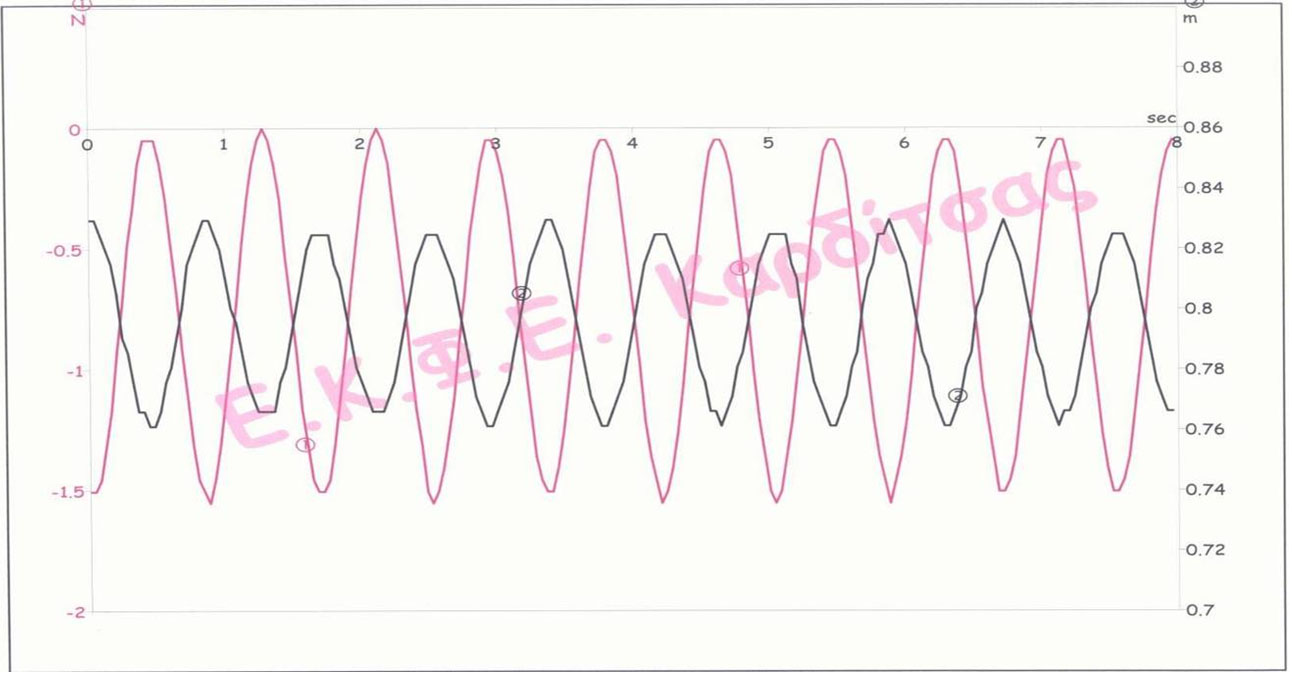
12. Αν θέλουμε να βλέπουμε στη γραφική παράσταση λιγότερες περιόδους κάνουμε διπλό κλικ στο σημείο που θέλουμε να αρχίζει το διάγραμμα και διπλό κλικ εκεί που θέλουμε να τελειώνει και εμφανίζονται στα δύο αυτά σημεία βελάκια. Επιλέγουμε «Προβολή», «Μεγέθυνση» (ή κλικ στο κουμπί με τον μεγεθυντικό φακό και το +, αριστερά στη στήλη με τα εικονίδια) και εμφανίζεται γραφική παράσταση με το κομμάτι μόνο της καμπύλης που βρίσκεται ανάμεσα στα βελάκια.
13. Αν θέλουμε να σχηματισθεί η γραφική παράσταση F=f(x), επιλέγουμε «Προβολή», «Απεικόνιση Υ(Χ)», «Επιλέξατε Χ?», κλικ στο Γραμμική (Διάστημα_I/O-1) και ΟΚ.
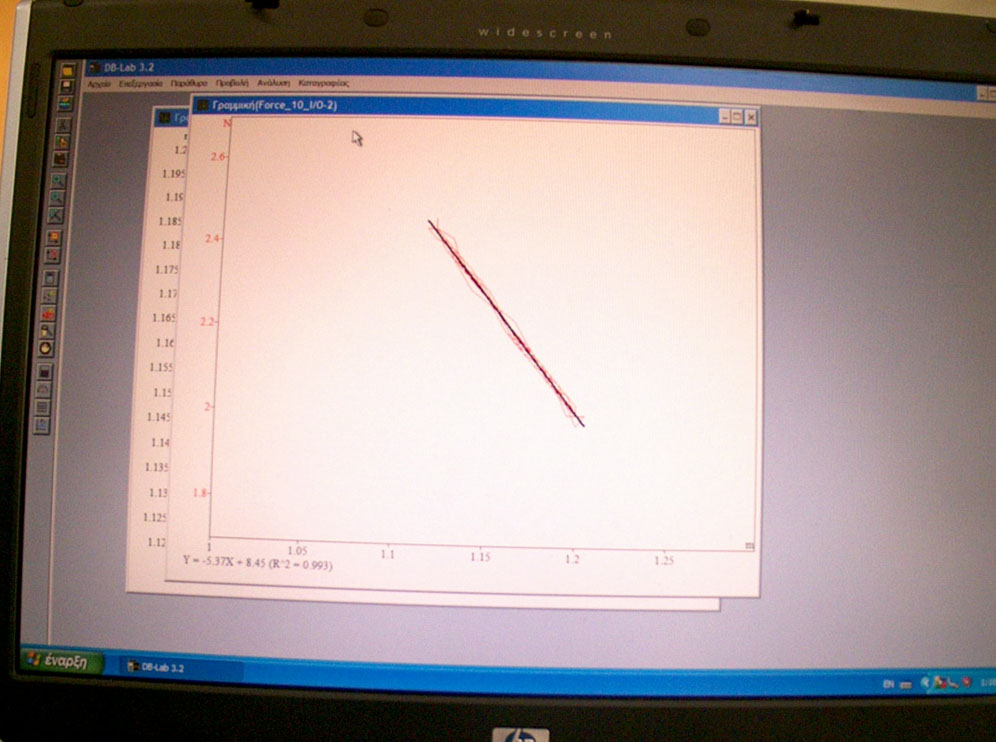
14. Επειδή δεν είναι πολύ καθαρή, λόγω σφαλμάτων, επιλέγουμε «Ανάλυση», «Γραμμική Παλινδρόμηση», στο παράθυρο «Επιλογή Δεδομένων» κλικ στο Δύναμη (SFS)_I/O-2 και ΟΚ. Εμφανίζεται μια γραμμή (α) και κάτω από την καμπύλη ένας τύπος (ο συντελεστής του Χ είναι η σταθερά του ελατηρίου και αν το R^2=1 σημαίνει ότι η σχέση είναι γραμμική).
Για να δούμε καθαρότερα τη γραμμή (α) επιλέγουμε «Προβολή», «Οθόνη?», στο παράθυρο «Επιλογές Μορφής παραθύρου», στα Χαρακτηριστικά γραφήματος, Επιλογή " Γραμμική Παλινδρόμηση (Γραμμική (Δύναμη (SFS)_I/O-) " ΟΚ, Χρώμα " στο παράθυρο «Χρώμα» επιλέγουμε έστω το κόκκινο" ΟΚ, Πάχος Γραμμής " 3 και ΟΚ.
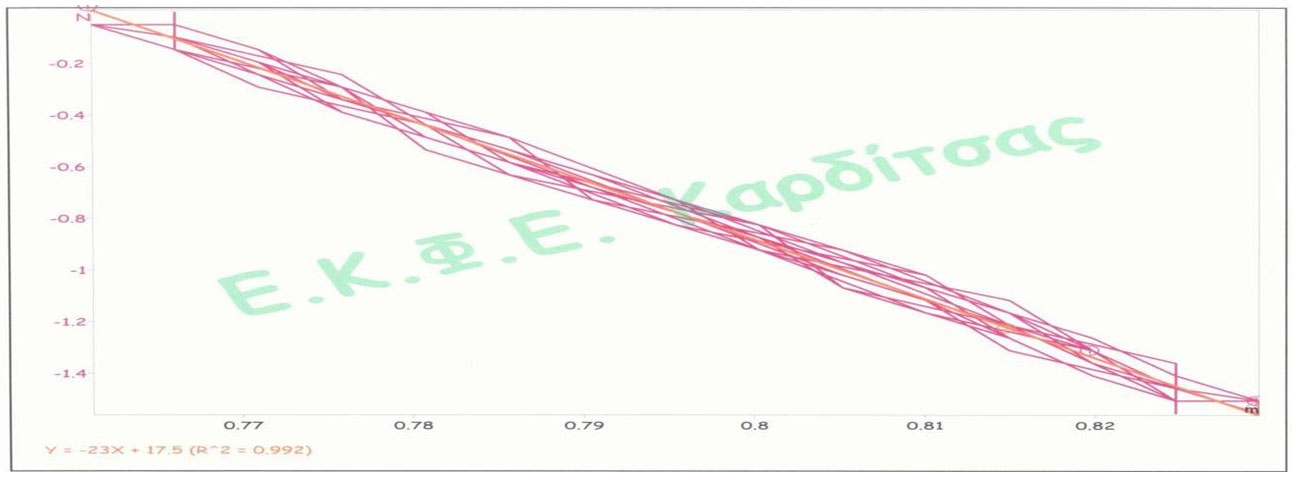


ΣΗΜΕΙΩΣΗ: Ακολουθούμε την παραπάνω πειραματική διαδικασία χρησιμοποιώντας το μπλε ελατήριο (με Fmax=2Ν και xmax=40cm, όπου xmax είναι το μέγιστο μήκος του ελατηρίου όταν κρέμεται το μέγιστο επιτρεπτό φορτίο Fmax).
Τη σταθερά k του ελατηρίου υπολογίζουμε από το νόμο του Hooke. Αφού κρεμάσουμε κάποιο βάρος στο ελατήριο μέχρι να ξεκολλήσουν οι σπείρες του, τοποθετούμε διαδοχικά δύο ή τρία βάρη και μετράμε τις αντίστοιχες επιμηκύνσεις του ελατηρίου. Αφού ελέγξουμε την ισχύ του νόμου του Hooke (ΔF=k·Δx), από τον τύπο ή την αντίστοιχη γραφική παράσταση F=f(x) υπολογίζουμε τη σταθερά του ελατηρίου k. Βρίσκουμε k =5,45N/m.
Οι αριθμοί που ακολουθούν αντιστοιχούν στα βήματα της παραπάνω πειραματικής διαδικασίας:
1. m=101g=0,101Kg (δηλ. w=m·g=0,101·9,81=0,99N)
7. F01=251,466mN=0,251N (στον αισθητήρα δύναμης έχουμε κρεμάσει μόνο το ελατήριο και ο αισθητήρας δείχνει ένδειξη θετική, δηλ. σαν να του ασκώ δύναμη προς τα πάνω)
F02=-1,233N (στον αισθητήρα δύναμης έχουμε κρεμάσει στο ελατήριο και το σώμα)
F0=|F02+F01|=0,982Ν
x0 =0,580m
9. T=880,00ms=0,88s
10. a) C1=-1 και C2=0,982 και β) C1=1 και C2=0,580
13. k=5,37 N/m (1,5% απόκλιση από την τιμή που μετρήσαμε με το νόμο του Hooke)

Το υλικό της σελίδας σε αρχεία για αποθήκευση: 1. Οδηγός ΕΚΦΕ (doc) 2. Εικόνες


















